Developing a Software Renderer Part 4

I added a vertex processing stage to the software renderer and implemented perspective correct texture mapping.

Vertex Processor

The vertex processor need to be able to process a list of input primitives, transform and process them using a vertex shader, map and clip them to the viewport, cull backfacing triangles and finally pass the primitives on to a rasterizer.

Similarly to the pixel shader I implemented a vertex shader system, where one can define the vertex shader as a static C++ class and set the shader using a function.

It is possible to set up various vertex attribute arrays using

v.setVertexAttribPointer(0, sizeof(VertexData), &vdata[0]);

The vertex shader than receives an array of vertex attribute pointers as inputs and can process these. This is similar to OpenGL when using vertex arrays with GLSL.

A simple vertex shader looks like this:

class VertexShader : public VertexShaderBase<VertexShader> {
public:
  static const int AttribCount = 2;

  static mat4f modelViewProjectionMatrix;

  static void processVertex(VertexShaderInput in, VertexShaderOutput *out)
  {
    const ObjData::VertexArrayData *data = static_cast<const ObjData::VertexArrayData*>(in[0]);

    vec4f position = modelViewProjectionMatrix * vec4f(data->vertex, 1.0f);

    out->x = position.x;
    out->y = position.y;
    out->z = position.z;
    out->w = position.w;
    out->pvar[0] = data->texcoord.x;
    out->pvar[1] = data->texcoord.y;
  }
};

Triangle Clipping

Points, Lines and Triangles that are feed into the vertex processor need to be clipped to the view-frustum before they can be passed to the rasterizer. This is especially important for primitives which cross the near clipping plane. If the primitives are not clipped there will be artifacts in the rendering.

For triangle clipping I implemented the Sutherland–Hodgman algorithm.

I used the following code:

class Helper {
public:
  static VertexShaderOutput interpolateVertex(const VertexShaderOutput &v0, const VertexShaderOutput &v1, float t, int attribCount)
  {
    VertexShaderOutput result;
    
    result.x = v0.x * (1.0f - t) + v1.x * t;
    result.y = v0.y * (1.0f - t) + v1.y * t;
    result.z = v0.z * (1.0f - t) + v1.z * t;
    result.w = v0.w * (1.0f - t) + v1.w * t;
    for (int i = 0; i < attribCount; ++i)
      result.avar[i] = v0.avar[i] * (1.0f - t) + v1.avar[i] * t;

    return result;
  }
};

class PolyClipper {
private:
  int m_attribCount;
  std::vector<int> *m_indicesIn;
  std::vector<int> *m_indicesOut;
  std::vector<VertexShaderOutput> *m_vertices;
  
public:
  PolyClipper()
  {
    m_indicesIn = new std::vector<int>();
    m_indicesOut = new std::vector<int>();
  }

  ~PolyClipper()
  {
    delete m_indicesIn;
    delete m_indicesOut;
  }

  void init(std::vector<VertexShaderOutput> *vertices, int i1, int i2, int i3, int attribCount)
  {
    m_attribCount = attribCount;
    m_vertices = vertices;

    m_indicesIn->clear();
    m_indicesOut->clear();
    
    m_indicesIn->push_back(i1);
    m_indicesIn->push_back(i2);
    m_indicesIn->push_back(i3);
  }

  // Clip the poly to the plane given by the formula a * x + b * y + c * z + d * w.
  void clipToPlane(float a, float b, float c, float d)
  {
    if (fullyClipped())
      return;

    m_indicesOut->clear();

    int idxPrev = (*m_indicesIn)[0];
    m_indicesIn->push_back(idxPrev);

    VertexShaderOutput *vPrev = &(*m_vertices)[idxPrev];
    float dpPrev = a * vPrev->x + b * vPrev->y + c * vPrev->z + d * vPrev->w;

    for (size_t i = 1; i < m_indicesIn->size(); ++i)
    {
      int idx = (*m_indicesIn)[i];
      VertexShaderOutput *v = &(*m_vertices)[idx];
      float dp = a * v->x + b * v->y + c * v->z + d * v->w;

      if (dpPrev >= 0)
        m_indicesOut->push_back(idxPrev);

      if (sgn(dp) != sgn(dpPrev))
      {
        float t = dp < 0 ? dpPrev / (dpPrev - dp) : -dpPrev / (dp - dpPrev);

        VertexShaderOutput vOut = Helper::interpolateVertex((*m_vertices)[idxPrev], (*m_vertices)[idx], t, m_attribCount);
        m_vertices->push_back(vOut);
        m_indicesOut->push_back((int)(m_vertices->size() - 1));
      }

      idxPrev = idx;
      dpPrev = dp;
    }

    std::swap(m_indicesIn, m_indicesOut);
  }

  std::vector<int> &indices() const
  {
    return *m_indicesIn;
  }

  bool fullyClipped() const
  {
    return m_indicesIn->size() < 3;
  }

private:
  template <typename T> int sgn(T val) 
  {
      return (T(0) < val) - (val < T(0));
  }
};

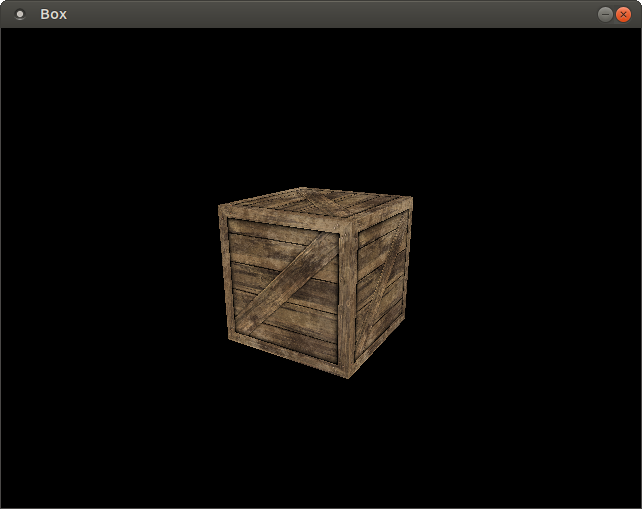
Perspective Correct Parameter Interpolation

Until now the per vertex parameters have been interpolated in an affine/linear way across the triangle. It looked good when we just used the rgb color but when we interpolate texture coordinate and use the coordinates to put a texture on an object we will notice that something is wrong.

To do perspective correct parameter interpolation we have to interpolate 1/w across the triangle and for each parameter interpolate p/w. Then per pixel we have to compute p' = p/w / 1/w = p/w * w.

The end result looks like this:

Checkout the source at my github repo.

Twitter  facebook  Google+