Developing a Software Renderer Part 1

Today software rendering has mostly been replaced by GPUs but there are still places where it can be useful.

One example is software based occlusion culling (Software Occlusion Culling and Masked Occlusion Culling) where a software renderer is used to create a hierarchical z-buffer which is in turn used to test object visibility and prevent invisible stuff from being sent to the GPU.

I implemented my own compact software renderer/rasterizer with some nice features like pixel and vertex shaders in C++ and in this article I describe how I did it.

Setting Up The Environment

We need to create a window where we can render our stuff into. For this we will use SDL2. It works under Windows and Linux. My blog post Using SDL2 with CMake describes all the necessary steps required to setup SDL2 with CMake.

Once you have set this up you can remove the code which uses the SDL_Renderer and use the following to render directly to the screen without a renderer:

SDL_Surface *screen = SDL_GetWindowSurface(window);
SDL_FillRect(screen, 0, 0);
SDL_UpdateWindowSurface(window);

Drawing Pixels

Ultimately we want to rasterize a triangle. For this we need to be able to fill every pixel inside the triangle with some color. We need a putpixel function to accomplish this.

An implementation of such a function can be found here or here.

You can then draw a lot of pixels like this:

for (int i = 0; i < 10000; i++)
{
  int x = random() % 640;
  int y = random() % 480;
  int r = random() % 255;
  int g = random() % 255;
  int b = random() % 255;

  putpixel(screen, x, y, SDL_MapRGB(screen->format, r, g, b));
}

Rasterizing a Triangle

There are a lot of resources about triangle rasterization available online but I feel like a lot of that information is not very good.

Fortunately I was able to find two valuable resources about triangle rasterization that helped greatly.

• Triangle Rasterization
• Accelerated Half-Space Triangle Rasterization

The interested reader should read both of those resources to understand the inner workings of the rasterizer.

Simple Filling

I decided to implement a rasterizer based on edge equations. We can encapsulate the edge related operation in an EdgeEquation class.

struct EdgeEquation {
  float a;
  float b;
  float c;
  bool tie;

  EdgeEquation(const Vertex &v0, const Vertex &v1)
  {
    a = v0.y - v1.y;
    b = v1.x - v0.x;
    c = - (a * (v0.x + v1.x) + b * (v0.y + v1.y)) / 2;
    tie = a != 0 ? a > 0 : b > 0;
  }

  /// Evaluate the edge equation for the given point.
  float evaluate(float x, float y)
  {
    return a * x + b * y + c;
  }

  /// Test if the given point is inside the edge.
  bool test(float x, float y)
  {
    return test(evaluate(x, y));
  }

  /// Test for a given evaluated value.
  bool test(float v)
  {
    return (v > 0 || v == 0 && tie);
  }
};

We also want to interpolate colors across the triangle. Later we also want to interpolate texture coordinates and in the general case arbitrary per vertex attributes. For this we create a ParameterEquation class.

struct ParameterEquation {
  float a;
  float b;
  float c;

  ParameterEquation(
    float p0,
    float p1,
    float p2,
    const EdgeEquation &e0,
    const EdgeEquation &e1,
    const EdgeEquation &e2,
    float area)
  {
    float factor = 1.0f / (2.0f * area);

    a = factor * (p0 * e0.a + p1 * e1.a + p2 * e2.a);
    b = factor * (p0 * e0.b + p1 * e1.b + p2 * e2.b);
    c = factor * (p0 * e0.c + p1 * e1.c + p2 * e2.c);
  }

  /// Evaluate the parameter equation for the given point.
  float evaluate(float x, float y)
  {
    return a * x + b * y + c;
  }
};

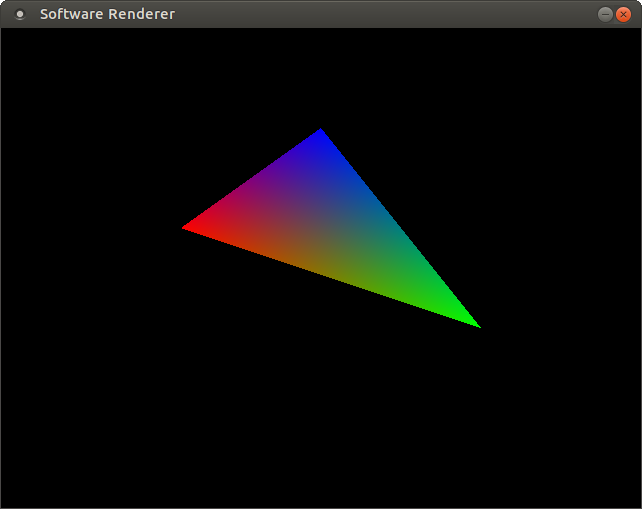
Then we can go on and rasterize the triangle. We compute the bounding box of the triangle, restrict it to the scissor rectangle, cull backfacing triangles and then fill all the pixels inside the triangle while obeying the fill rule with the tie-breaker as described in the references.

void drawTriangle(const Vertex& v0, const Vertex &v1, const Vertex &v2)
{
  // Compute triangle bounding box.
  int minX = std::min(std::min(v0.x, v1.x), v2.x);
  int maxX = std::max(std::max(v0.x, v1.x), v2.x);
  int minY = std::min(std::min(v0.y, v1.y), v2.y);
  int maxY = std::max(std::max(v0.y, v1.y), v2.y);

  // Clip to scissor rect.
  minX = std::max(minX, m_minX);
  maxX = std::min(maxX, m_maxX);
  minY = std::max(minY, m_minY);
  maxY = std::min(maxY, m_maxY);

  // Compute edge equations.
  EdgeEquation e0(v1, v2);
  EdgeEquation e1(v2, v0);
  EdgeEquation e2(v0, v1);

  float area = 0.5 * (e0.c + e1.c + e2.c);
  
  // Check if triangle is backfacing.
  if (area < 0)
    return;

  ParameterEquation r(v0.r, v1.r, v2.r, e0, e1, e2, area);
  ParameterEquation g(v0.g, v1.g, v2.g, e0, e1, e2, area);
  ParameterEquation b(v0.b, v1.b, v2.b, e0, e1, e2, area);

  // Add 0.5 to sample at pixel centers.
  for (float x = minX + 0.5f, xm = maxX + 0.5f; x <= xm; x += 1.0f)
  for (float y = minY + 0.5f, ym = maxY + 0.5f; y <= ym; y += 1.0f)
  {
    if (e0.test(x, y) && e1.test(x, y) && e2.test(x, y))
    {
      int rint = r.evaluate(x, y) * 255;
      int gint = g.evaluate(x, y) * 255;
      int bint = b.evaluate(x, y) * 255;
      Uint32 color = SDL_MapRGB(m_surface->format, rint, gint, bint);
      putpixel(m_surface, x, y, color);
    }
  }
}

Conclusion

The simple implementation works, but performance is not great. It can be improved by a block based approach that allows us to discard blocks outside the triangle faster and skip some test when the block is completely inside the triangle. This will be covered in the next part of this series.

Other improvements are the support of texture coordinates and other per vertex parameters, perspective correct parameter interpolation, multi-threaded rasterization and a pixel shader framework that allows us to configure the per pixel operations in a flexible manner to support texture mapping, alpha blending and other stuff. These are also topics that will be covered in the next posts.

Continue reading on Part 2.

Checkout the source at my github repo.

Twitter  facebook  Google+